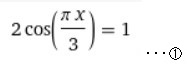
これは微細構造定数の近似式を連分数の形式で表現しているときに見つけたことなのですが、左の余弦関数の式(この式を①とします)の解が左下の式になります(この式を②とします)。

ここで、Zは整数の集合です。よく知られた結果ですが、②の式は、nが自然数の場合、6n-1および6n+1は2および3を除く素数を表現可能です(但し、素数以外の数字も含みます)。
また、①の式の解としては6n+5のかたちも含みます。
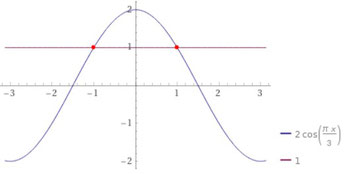
ここで、①の式をグラフで表すと、y=2cos(πx/3)とy=1との交点で表現される点の集合となります。
別な表現をすれば、2cos(πx/3)-1=0の零点の集合ともいえますね。

上記の交点のx軸上における分布は左図のイメージになり、2および3以外の素数は2cos(πx/3)=1の解として求められる集合の部分集合となります。
丁度、余弦波の交点の間隔がうまく素数の間隔とあてはまるのでしょうが、これはちょっとした発見かなと思い、恩師に相談したところ、多分偶然ではないかとの結論に至りました(^_^;)
上記の式は素数以外の数も含みますが、ある周期の波の無限に続く零点の集合の部分集合が素数の集合というのはちょっとロマンのある話だなと思っています。

ここで、もうちょっとだけ頑張ってみます(^_^;)
n番目の素数(Pn)を解として持つ多項式が存在するならば、③のような式になると思います。ここで自然数の部分集合である素数を勝手に整数の範囲まで拡大解釈して負の符号を持つ素数も含めて解とする多項式を考慮すると次の④のような式になると思います。

④の式では、x^2-Pn^2の無限積として表現されておりますね。

ここで、④の多項式の1からnまでの部分積を⑤のようにf(x)とおいて総乗の式を展開すると、恐らく⑥のようになります。
見るのも辛そうな式ですね(^_^;)
このような多項式の展開は多項定理関連でいけるかなと思ったのですが、よいものが見つけられなかったので自力で展開しました。ですので計算間違いの恐れがあり、その際は何卒ご容赦くださいませm(_ _)m
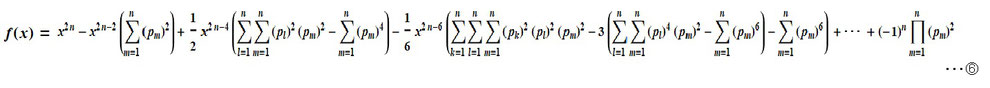
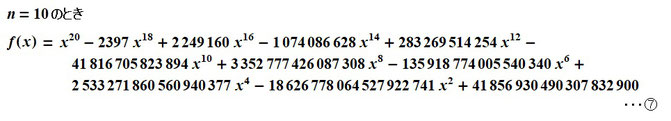
一般項としてのnではいまいちイメージがつかみにくいので、n=10のときのf(x)を展開してみたものが⑦になります。
ここまでくると、2cos(πx/3)-1=0を級数展開してみたくなりますよね(^_^)
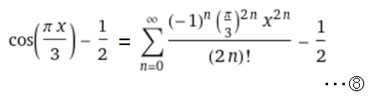
2cos(πx/3)-1を2で割って級数表現したものが⑧の式になります。
ここで、⑦と同様に、n=10のときの展開式を見てみましょう。
下記⑨がその展開式になりますが、初項のの係数が邪魔ですね・・・。
これは、(π^20)/(20!*3^20)が係数として掛かっているので、この値で両辺を割ってみましょう。


両辺を(π^20)/(20!*3^20)で割ったものが⑩になります。ちょっとだけ見やすくなりましたね(^_^;)
⑦と⑨(または⑩)は係数の大きさに違いはありますが、ともにxは2nの冪乗のかたちになっており、第2項以降の符号はマイナスとプラスを繰り返している点など似たかたちをしてますね。
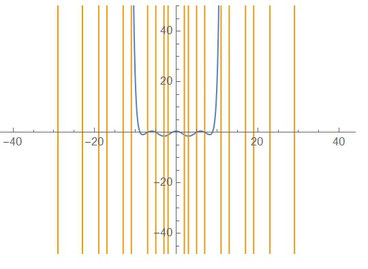
ただ、⑦と⑨をグラフ表示してみると、⑦:オレンジ、⑨:ブルーで表示された曲線となり、⑦のy軸方向の振幅が非常に大きいことが分かります。これはn=10という小さな数字でグラフ表示したことにも原因があるかもしれませんが、この多項式自体の係数の値の補正(全体を大きな数で割る)等の検討をする必要があるかもしれないですね。
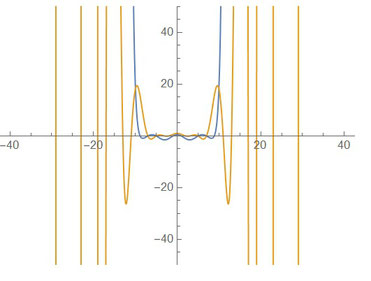
そこで、⑦を末尾の定数項である41856930490307832900で割ったもの:オレンジと⑨:ブルーをグラフ表示したものが左図になります。
x=0付近の振動は比較的小さくなりましたが、x=±10を超えたあたりから振動が大きくなります。

ここで少し安直ですが、f(x)を末尾の定数項で割ったものをg(x)とおき(⑪)、n=100000のときのg(x)を表したものが左図のグラフになります。
値は異なりますが、n=±10を超えたあたりから振動が大きくなる傾向は上図と同じですね。尚、管理人の環境ではグラフ描画に大変時間がかかったり、途中で警告も出たりしたのでこれが限界かな・・・(^_^;)
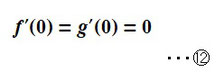
尚、今回作成した多項式f(x)およびg(x)はグラフで見て分かるとおり、y軸に対して対象形になっておりますので、⑫のようにそれぞれの式を微分したものはx=0で値0をとると思います。
今回はg(x)のかたちでn=100000までしか試してませんので、nの値をもっと大きくすればどうなるかわかりませんが、傾向としては同じだと思います。でも、これ以上の調査はちょっと難しいですね~(^_^;)
コメントをお書きください