以前、「素数を解とする式について」というブログ記事を記載しましたが、その続編です。
あの後、ふとしたことで思いついた式がありました。
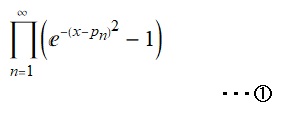
それが左図①の式で、以前は素数を解とする多項式についてでしたが、グラフ表示したところ変数xの値(この場合は絶対値)が大きくなるにつれて病的に振幅するので、これは厳しいなと思ったのですが、それならxの値が大きくなってもyの値がとも連れで大きくならなければいいんじゃないの、ということで考えついたものです。要するに、ガウス分布からの思いつきで、eの冪乗項(x - Pn)をマイナス2乗したものから1を引いたかたちの総乗の式です(ここでPnはn番目の素数を表します)。
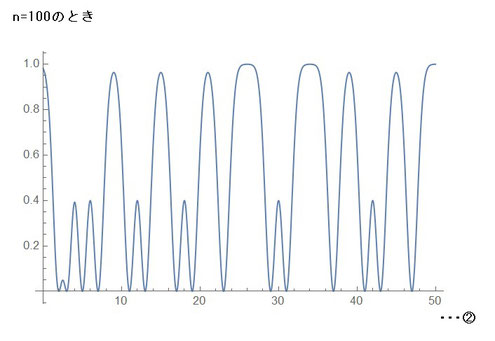
①の式でn=100としたときのグラフが左図②です。
このグラフを描画していると、管理人の計算環境では警告がでました・・・(^_^;)
値の発散は無いようですが、歪なかたちをしてますね・・・。
やはり、無理があるのかなと思っていたところ、そういえば先のブログで2cos(π*x/3) = 1のかたちの式は素数を含む6n - 1および6n + 1を解としていることを思いだし、せっかくなので、その式に欠けている素数解(2および3)の項である(e^(x - 2)^2 - 1)(e^(x - 3)^2 - 1)を付加してみることにしました。
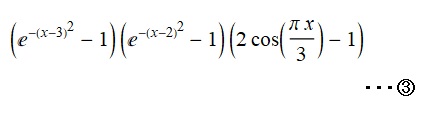
それが左図③の式になります。
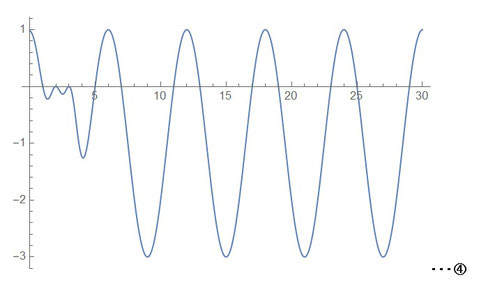
③の式をグラフにしたものが左図④になります。
2と3が解となっているようで、なかなかよさげですね(^o^)
しかし、この③の式では素数の他に合成数も含んでおり、悩みの種です・・・。
その合成数を解から外す方法はあるのか・・・と思っていたところで、信号処理等で使われるsin(π*x)/π*xを思い出しました。
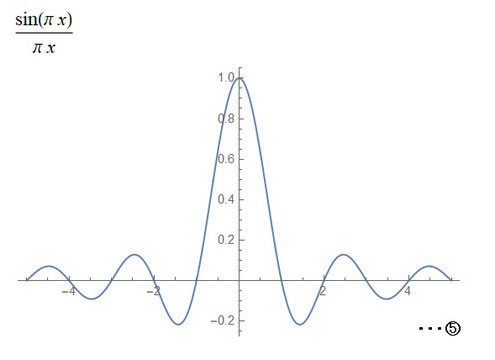
それが左図⑤の左上の式で下の図がそのグラフになります。
⑤の式はx = 0の近傍で分子も分母も0に近づきますが式の値としては有限値となっております。
もしかしてこれが応用できるかな、と思い(x - 合成数)で割ってみることにしました。
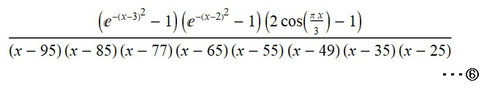
③の式を6n -1 および6n + 1の形式の100までの数で合成数をピックアップし、それを(x - 合成数)の積のかたちで除算したものが左図の⑥になります。
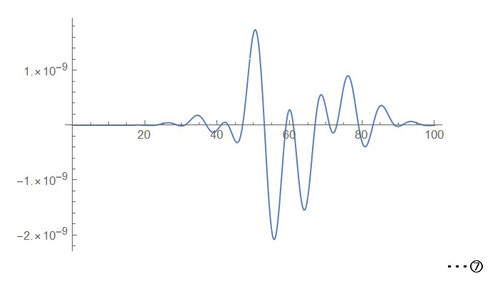
⑥をグラフにしたものが左図⑦になります。
この時点では警告は出ませんでした(^_^;)
値は小さいですが、なんとなくよさげですね。
⑥で45から60あたりが合成数が比較的多いので、その部分を別のグラフで表示してみました。
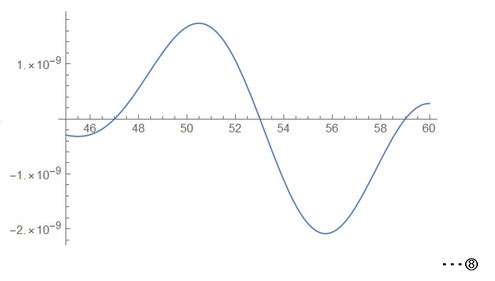
xの範囲を45から60までとしたものが左図⑧のグラフです。
表示にあたり、少々警告は出ましたが、合成数:49、55をうまくかわしてくれたようです(^_^)
ただ、6n - 1および6n + 1の形式の数の中には、合成数はおそらく無数にあると思われるのでその点は問題ですが、合成数を増やしてみるとどうなるか試して楽しむ分にはよさげですね(^_^)
コメントをお書きください
n (水曜日, 07 12月 2022 15:52)
これ面白い