先日、コンパスと定規による角の三等分(近似)線について記載しましたが、ネットを漁っていたところ、過去に角の三等分近似線の作図についての論文(千葉工業大学:太田先生・南先生共著)が見つかり、その中に掲載されていた「田中法」がシンプルで作図において紙面もそれほど広く使わずに済むため、その内容をご紹介させて頂きます。
他にも幾つかの優れた方法が記載されているのですが、シンプルさと省紙面という点で田中法が魅力的でした(^o^)
※論文のリンクについては掲載許可を取っていないため割愛しますm(_ _)m「角の三等分近似画法」でググれば見つかると思います。

分割対象となる角をθとし、角θをなす線分を適当に延長し、原点Oを中心としてコンパスで円弧➊を引きます(左図①参照)。
延長した線分と円弧の交わる点をAおよびBとします。
さらに線分OBを四分割する点および線分ABを三分割する点をとり、線分OB上で原点Oに近い点をC、線分AB上で点Bに近い点をDとします。
ここで点Cから点Dを通る直線が、円弧➊と交わる点をEとします。この点Eと原点Oを結ぶ線分OE(図①では赤色の線)がθ=∠AOBを近似的に三等分する線分となります。
図①ではθ=60°のときですが、この場合∠BOEは約19.96°となります。
この作図法では0°<θ≦90°において、θの値とそれに対して求められた∠BOEの値は概ね次のようになります。
θ=30°のとき、∠BOE=9.999°
θ=45°のとき、∠BOE=14.99°
θ=60°のとき、∠BOE=19.96°
θ=90°のとき、∠BOE=29.67°
上記を見てわかると思いますが、角度が大きくなるに従い近似精度が落ち、θ>90°の場合はさらに大きく近似精度が落ちます。
例えば、θ=120°のときの場合に上記と同様にして角の三等分の近似値をとると値は38.21°となり、θ=150°のときの値は41.04°となります。
従って、上記論文では「田中法」の場合、適用対象の角度は0°<θ≦90°と記載されております。
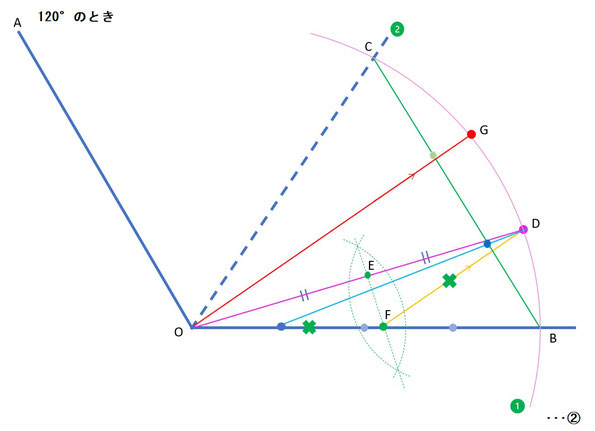
しかし、管理人のようなひねくれ者は左図②のように、「角度を半分にして三等分の近似線を作図しておいて、後で倍にすればいいんじゃない?」みたいな考え方をしてしまいます(^_^;)
まず、∠AOBを二等分する直線➋(図②では破線)を引き、図①と同様に円弧➊を引きます。直線➋と円弧➊との交点をCとし、線分OCを取得します。
線分OCおよびOBとのなす角である∠BOCを三等分する近似線OD(図②では濃いピンク色の線)を図①と同様の方法で取得します。
その後、その線分ODを二等分する点Eから線分OBに対して垂線の足(図②では点線)を引き、その交点Fとすると、△DOFは二等辺三角形になります。
∠DOF=∠FDOなので、∠DFBは∠DOBの二倍角になり、線分DF(図②ではオレンジ色の線)に対して平行な原点Oを通る直線を引けば、その直線と円弧➊との交点Gと原点Oとの線分OG(図②では赤色の線)がθ=∠AOBを三等分する近似線となります。
このように考えると、先日ブログに記載した方法でも使えるかな~なんて今更ながら思ったりもします(^_^;)
コメントをお書きください