素数の総乗による式を調べていたところ、下図①のような既知の結果を見つけることができました。
※Pnはn番目の素数を表しております。
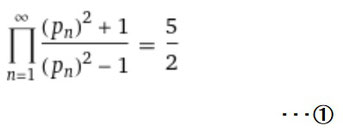
とてもシンプルで美しい結果だなと思い、この結果からヒントを得て、下図②のような式を得ました。

左辺は素数Pnのs乗(s > 1)を分子で+1、分母で-1を加算した総乗の式です。
右辺はゼータ関数ζ(s)で表現されており、右辺 = ζ(s)^2/ζ(2s) となります。
①は、②におけるs = 2の場合の結果になりますね。
ζ(2) = (π^2)/6 , ζ(4) = (π^4)/90 により ζ(2)^2/ζ(4) = {(π^4)/36}/{(π^4)/90} = 5/2
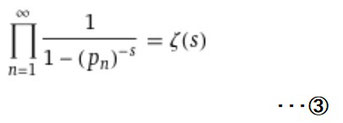
②のゼータ関数までの導出については、③のオイラー積とゼータ関数の関係式を念頭におき、下図④の総乗内の式変形を実施しすれば②が導出できます。

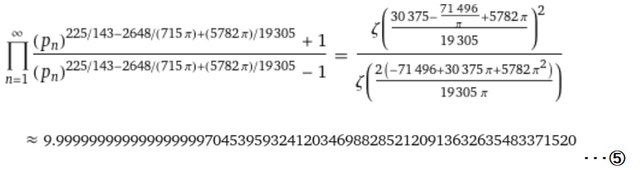
実は、この結果を使うと以前「ほとんど整数」というブログ記事の最後に記載した数10の近似式よりももう少し精度の高い近似式を得ることができます(左図⑤)。
ただ、式としてはあの記事に掲載した近似式の方が愛着が有り、管理人がいかにに恣意的に記事を書いているかよく分かりますネ(^_^;)
コメントをお書きください