先日、コンパスと定規による線分の三等分割についてブログに記述しました。しかし、その後、「コンパスと定規による角の三等分線」について何も考えたことが無かったことにはたと気づきました。割と子供の頃からコンパスと定規による角の三等分線の作図については(一般的に)不可能であることを知っていたので、できないものについて考えても仕方ない、と思っていたからです。
しかし、微細構造定数の近似式を嫌になるほど作ってみたことが災い?し、コンパスと定規による角の三等分線の作図も近似的にどこまで追い込めるかトライしてみるのも面白いかも、と思ってしまいました(^_^;)
できないことが分かっているにもかかわらず、角の三等分線の作図方法を考えている人を(角の)三等分家とか三等分屋と呼ぶそうですが、その三等分家の精神に則り、敢えてトライしてみました(^_^)
古来より数多の人々がチャレンジしているので既出の方法である可能性が高いですが、分割される角をθとしたときに、0°<θ≦90°の場合と90°≦θ≦180°の場合の2つのケースで作図方法を考えてみました。
※角度については大きさがイメージしやすいように、敢えてラジアンではなく度数を使っております。
また、予めことわっておきますが、掲載されている図はフリーハンドで書いたイメージ図であり、厳密さに欠けます(^_^;)
あれ、ちょっとこの図形おかしくない?みたいなものもありますので、それについてはご容赦くださいませm(_ _)m
ケース1:0°<θ≦90°の場合
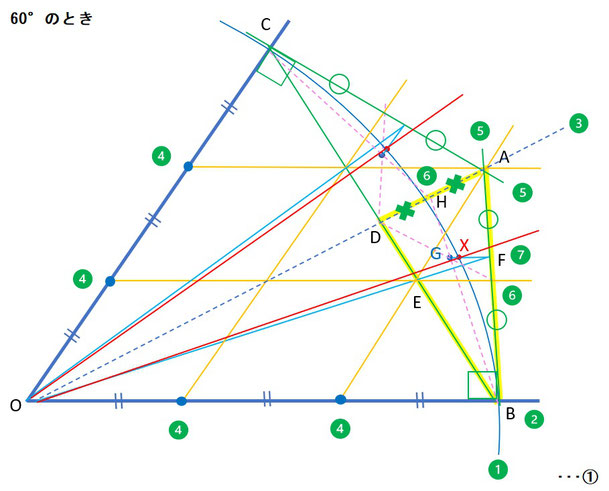
ケース1の場合、左図のような方法を考えてみました。これは分割される角に対してコンパスにより円弧を描き、その円弧を可能な限り1:2の比に近くなるように分割する点を探すものです。
作図方法としては原点をOとし、分割する角の線分を延長し、その線分の適当な位置に図の中で緑色の白抜きの番号:❶で示されているような円弧を書きます。その後、円弧とそれぞれの線分との交点をBおよびCとし、線分BCの中点と原点Oを通る線分を引きます(図では❸の破線です)。
ここで、先回のブログで記載した線分の三等分割方法により、線分OBおよびOCを三等分する点を書き、その点を通り、対辺の線分と平行になるような線分をそれぞれ引きます(図では❹の線分です)。
また、❸を通り、線分OBおよびOCとそれぞれ直角に交わる線分を引きます(図では❺の線分です)。この線分の交点をAとし、❸と線分BCの交点をDとすると、黄色の太線で示したような直角三角形ABDができます。この△ABDを半分の長さの円弧が通るため、これを可能な限り1:2に近い比率で分けたいと思います。
ここで、辺ADおよび辺ABの中点を通り、対角に線分をそれぞれ引きます(図では❻のピンク色の破線になります)。その線分の交点は△ABDの重心G(図では青色の点)になります。
ここでちょっと一手間ですが、辺BDと❹で引かれた線分の交点をEとすると、線分OEを延長して辺ABと交わりますが、その交点をFとします。その点Fから重心Gに対して引いた線分と円弧との交点をX(図では赤色の点)とします。
θが60°の場合、この線分OXとOBのなす角∠BOXを計算すると約19.85°になります。θを三等分した値:20°に近い値になります。
また、線分BOとOGのなす角∠BOGも約20.17°であり、こちらも20°に近い値です。
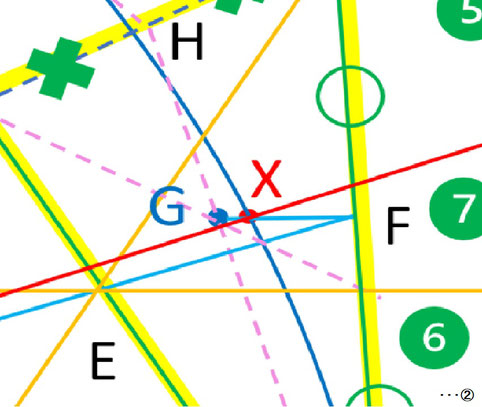
上図では重心Gと点Xとの位置が近く分かり難いので、拡大したものが左図になります(これでも分かり難いですね(^_^;))。
重心G(青色の点)は△ABDの各辺の中点とその対角を結ぶ線分(図ではピンク色の破線)を1:2に分割しますので、円弧がこの線分(線分ADの中点Hを通るピンク色の破線の線分HB)に近い長さでかつ近い位置を通るケースであれば、重心Gが三等分割における近似点になります。
しかし、ここでその位置関係や円弧の長さに若干開きがあるようであれば、さらに線分DBを1:2に分割する点Eを通る線分OFと重心Gとの線分と円弧の交点であるX(赤色の点)が近似点である可能性が高くなります(線分EFと円弧との交点では三分割点から少し離れるため、重心Gとの間をとった点となっております。一種の補正点ですね)。
θの値が大きいほど、重心Gによってなす角∠BOGと角の三等分割値との乖離は大きくなりますが、逆にθの値が小さいと、角の三等分割値との乖離は小さくなります。
それでは、θがその他の値のときを見てみましょう。
※以下の図では引き続き、重心Gを青色の点、円弧上の交点Xを赤色の点で表現しております。また、原点Oから重心Gを通る線分OGは線分OX(赤色の線)とほぼ重なるケースが多く紛らわしいため、線分OGについては敢えて図中に記入しておりません。
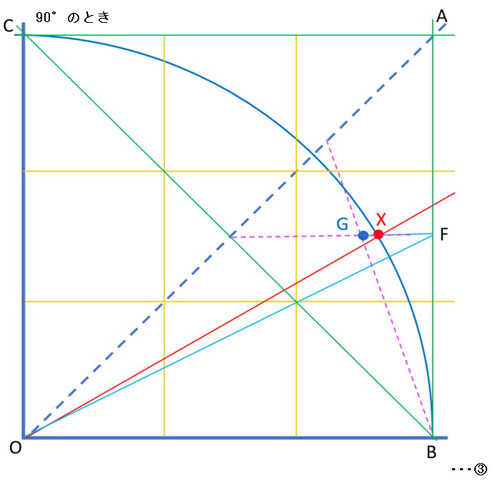
左図は、θが90°のときのイメージ図です。
このとき、重心Gと線分FGと円弧との交点XはGと辺ABの中点(この場合F)との線分上にあり、線分FGとOBは平行なので、このとき∠BOXはθの三等分の角度:30°と同じ値になります。
これは左図から分かるように、θ=90°の場合、線分FBが円弧の半径の半分の長さであり、円弧の半径:点Xから線分OBに引いた垂線の足の長さ=2:1となるため、∠BOXは30°となります(つまりsin30°=1/2)。
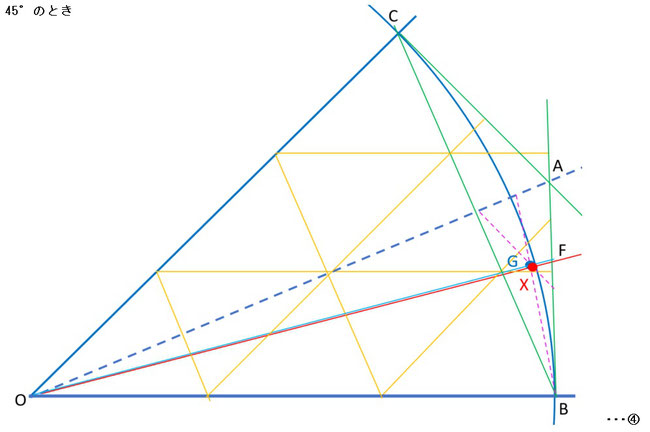
左図は、θが45°のときのイメージ図です。
60°のときのーメー次図でも重心Gと円弧上の点X位置関係は極めて近くなります。
θの三等分の角度:15°ですが、このとき、∠BOXの値は約14.92°となります。
ですが、線分OGとのなす角∠BOGを計算すると約15.06°となり、極わずかですが∠BOXよりも三等分の値に近いものになります。
θの角度が小さくなるに従い、重心Gの方が三等分の近似点となります。

ケース1の最後として、θが30°のときのイメージ図になります。
θ=45°で触れたように、この場合の角の三等分の値は10°ですが、∠BOXの値が約9.976°であるのに対し∠BOGの値が約10.01°となり、重心Gが近似点となります。
※重心Gと点Xがほぼ重なってしまうので、イメージ図上では少し距離をとって作図しております。
また、敢えてイメージ図は掲載していないですが、90°を超えると円弧と△ABDの図形的な関係も変わってきて、120°のときに∠BOXを計算すると、値は約41.41°となり三等分である40°とそれなりに近い値ではありますが、辺ABの中点から原点Oに引いた線分とBOとのなす角の値:約40.89°の方が近似値となり、徐々に関係性が崩れてしまうので、この方法は90°までかなぁ、と思っております。
ケース2:90°≦θ≦180°の場合
ケース2の場合、左図のような方法を考えてみました。
分割対象となる角の線分を延長し、適当な半径の円弧(図では緑色に白抜き数字の❶)を書きそれぞれの線分と円弧との交点をXおよびYとします。
さらに、円弧❶より半径の短い円弧(❶の半分の半径の円弧が簡便かと思います)の円弧を書き、これを❷とします。
点XおよびYにてコンパスを使い、∠XOYを二分割する線分を引きます(図では❸となります)。さらに円弧❶と❸との交点を使い、∠XOYを四分割する線分をそれぞれ引きます(図では❹になります)。
線分❹と円弧❷の交点をそれぞれBおよびCとし、線分BCを一辺とする正三角形の頂点Aをコンパスを使い取得し、定規により正三角形ABCの各辺となる線分を引きます。
ここで正三角形の各頂点A,B,Cを中心とし、△ABCの各辺の半分の長さの半径の円を作成します(最低限、点Aを中心とする円があればOKです)。
作成した点Aを中心とする円に接し、辺BCに平行な線分を引きます(図では❻になります)。
また、❻に対し辺BCの端点BおよびCを通る垂線の足を引きます(図では❼になります)。
❻および❼との交点をそれぞれB'およびC'とし、線分B'C'を一辺とする正三角形の頂点A'をコンパスを用い、❸の線分上にとります。
それから正三角形A'B'C'を作成します。図から分かるように、△A'B'C'は△ABCを180°回転したものになります。
ここで作成した△A'B'C'と△ABCとの交点をそれぞれDおよびD'とします。
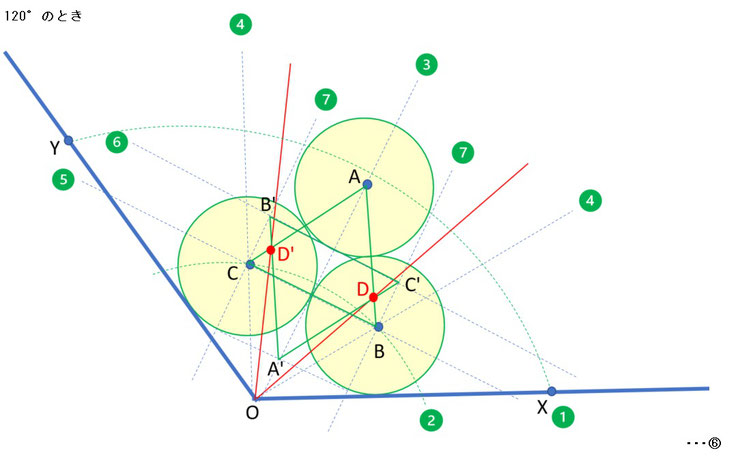
この交点Dと原点Oとの線分ODと線分OXのなす角∠DOXが求める三等分の角度(この場合、θ=120°なので、40°)の近似値にまります。
∠DOXの角度を計算すると、約39.4°になります。

左図はθ=180°のときになります。
イメージ図を見ても分かるように、正三角形により180°の三等分である60°で分割されます。
この3つの円と二つの正三角形の関係は分割対象の角度が変わっても保たれるため、このイメージを元に上図のような方法を思いついた次第です。

左図はθ=150°のときのイメージ図です。
この方式はθの角度が180°に近いほど近似精度がよいので、このときの∠DOXの値は約49.8175°で、三分割の角度50°に近い値になります。
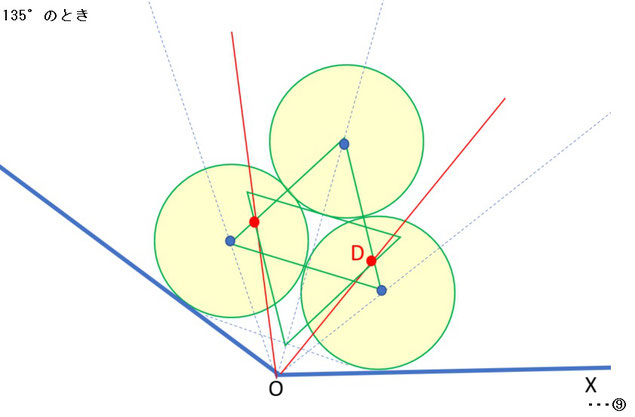
左図はθ=135°のときのイメージ図です。
このときの∠DOXの値は約44.55123°であり三分割の角度45°に近いですが、150°のときより近似精度が落ちてきていますね。
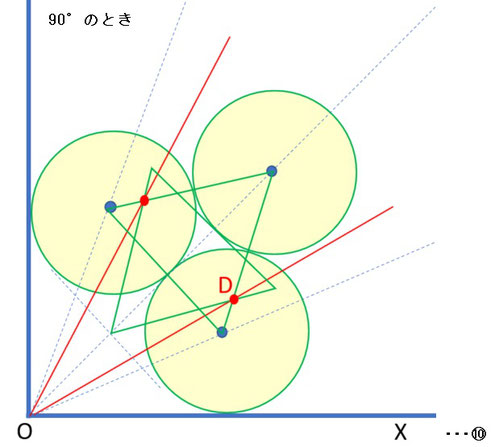
左図はθ=90°のときのイメージ図です。
このときの∠DOXの値は約29.16°で、θを三等分した値である30°にそれなりに近いものになります。
但し、ケース1のθ=90°の場合と比べると近似精度は落ちますので、まぁこの作図方法ではこのあたりが限界かな、と思います。
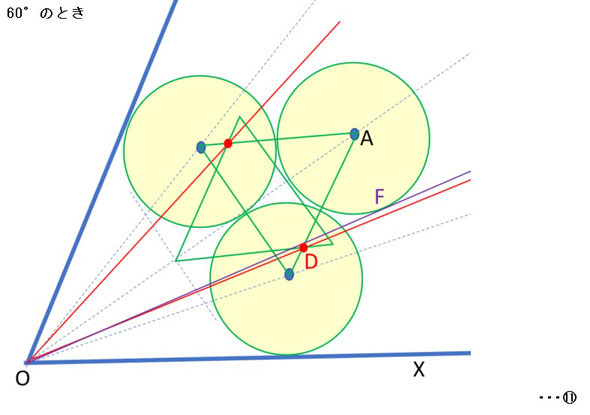
というのも、左図(θ=60°)の場合を計算すれば分かるのですが、このとき∠DOXの値は約19.11°であり、三分割の値である20°にそこそこ近いのですが、実は点Aを中心とする円と原点Oとの接線(円との接点をFとする)と線分OBとでなす角∠FOXは19.45°となり、∠DOXより∠FOXの方が近似値としてより近いものになってしまうのです。
最初、角の三等分線を近似できる作図法を考えるにあたり、この円の接線も候補として考えておりましたが、θのなす角が大きくなるにつれて近似精度が悪くなり、もっと近似精度の高い方法(ケース1)が見つかったのでお蔵入りした作図法です。
従って、ケース2の作図方法は90°から180°あたりで使用するのが適切かなと思います。
ちなみに、180°を超える角度については全く検討しておりませんのであしからず(^_^;)
今回、作図として無理であることが分かっていて敢えてトライしてみましたが、シンプルな図形の持つ「頑張ればなんとかできそうな」魅力(というか誘惑?)を改めて感じた次第です。言い換えれば、錬金術的な魅力というか・・・(^_^)
今回、作図以上に大変だったのが計算による角度の値算出でした。どこかで計算間違いしてないかどうか・・・ちょっと心配です(^_^;)
コメントをお書きください