
管理人は子供の頃に数学にまつわる発見を二つほどしております。発見といってもとるに足りないことですが、他に書くネタも思いつかないので、その当時を思い出しながら以下に記載してみます(^_^;)
まずは、今から遡ること40数年前の小学生で面積を習ったばかりの頃、一辺を2cmとする正方形▢を紙に書き、その中点で内接する菱形の正方形◇を書きました。▢の面積は2×2=4cm^2なので、◇の部分の面積は半分の2cm^2になります。なので安直に◇の一辺も半分だろうとたかをくくって定規で測ってみると、どうやっても定規の目盛りをあてると中途半端な数字になるので、測り方か図の書き方が悪いのかと悩みました。このとき初めて√2と出会ったのですね。
中学校に入って、あのときの数字は√2だったのか、と分かったときは、なにやら感慨深いものがありましたね(-_-)
ここから本題ですが、中学校でコンパスや定規を使って線分を二等分したり、二等辺三角形や正三角形などを書いて面積を求めたり等を習っている頃、数学の先生が線分の三等分について授業で話をされました。
その解説された方法としては、線分の一端から3で割り切れそうな長さの斜辺を引いて、斜辺の長さの1/3の点を斜辺上にとり、そこから分割対象の線分上に平行線を使って投影するものでした。
その時、先生はコンパスと定規を使って線分を三等分するには今のところこれくらいの方法しか知らなくて、三等分した結果もあまり芳しくない旨を仰られたので、他に方法がないか自分で考えてみることにしました。
そこで二つほど方法を思いついたのですが、一つは多角形を書いて複雑な補助線を引くものでどういったものか忘れてしまいましたが、もう一つは上図に示したような方法です(実際にはもう少し補助線的なものを引いていた記憶がありますが、内容としては同等です)。
三等分対象の線分をAとすると、辺Aに対し二等辺三角形(二等辺三角形でなくてもよいですが作図においてより簡便であり、さらにイメージしやすいのは正三角形ですね)となる斜辺を書き、それらを辺BおよびCとします。
そこで、BおよびCの中点からそれぞれの辺の対角の頂点に対して線分を引くと交点ができますが、これは辺ABCで構成される三角形の重心であり、図の赤色で示した線分を1:2に分割します(BおよびCのそれぞれの中点を結んでできる茶色の点線の線分および重心とでできる三角形と、重心と辺Aとでできる三角形は相似でその比は中点連結定理により1:2になるためです)。そこで分割された線分のうちで長い方の線分に対しコンパスを使って中点をとり、それらの点を平行線(この場合は辺Bに対し平行な線)を使ってAに引けば、Aを三等分割する点が取得できます。
この方法について後日、先生にご説明したところ褒めて頂けたので嬉しかったですね(^_^)
それから高校受験時に、英語の長文問題でガウスの小学校時代に1~100までの和の計算をあっという間にやってのけて先生を驚かした、という内容の文章が出題され、試験中にもかかわらず、いたく感心した覚えがあります。その時の計算方法は1+100=101、2+99=101、3+98=101、・・・50+51=101であり、1~100までの和は101×50=5050というものでした。
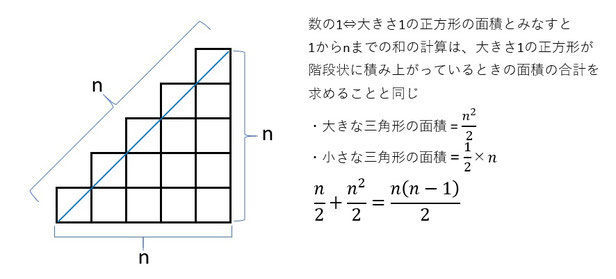
高校入学後、その計算方法について思い出し、自分は1~nまでの和を求める方法を考えてみようと思ったのでした。高校一年の冬のある日、こたつで寝転びながら考えて、左図のような方法でn(n+1)/2という式を思いつきました。数字の1を面積:1の正方形とみなすと、1から始まる自然数の和は図のような階段状の図形になるので、図で示されている辺の長さnの大きな三角形の面積:(n^2)/2およびノコギリの刃のようなn個の小さな三角形の面積:n*1/2の和が求める図形の面積になるので、自然数1~nまでの和=n(n+1)/2、というものでした。
これを思いついたときは、この結果を知っているのは自分だけ?みたいな感じでひとりでほくそ笑んでおりました。しかし、その後しばらくして数学で数列を習い、そこで公式として記載されているのを見てがっかりし、されにはこの結果は随分古くから知られていたものだということが分かったときには自分の情けなさに半笑いになったものでした(T_T)
とりとめの無いことを書き連ねましたが、昔を思い出しながら書くのも一興ですね(^_^)
コメントをお書きください