ファイゲンバウム定数

ある日、ネットを検索していて何気に気になる近似式を発見しました。

左記①は第1ファイゲンバウム定数の近似式でかたちもシンプルで値もよいものです。

そもそも、カオス理論のファイゲンバウム定数自体がもともと気になっていたのですが

先回のブログでも記載したように10という数字がいやに気になっていたので、気になるもの同士を組み合わせてみました(^_^)

※以下で使用するファイゲンバウム定数は差分方程式がZ=2のとき、つまりロジスティック写像の場合における値を指します。

10を①の近似式で冪乗してみたところ、第1ファイゲンバウム定数を10000倍（10の4乗というのが思わせぶり）した値に近いものになりました。偶然ですね～(^_^;)

それでは、第1ファイゲンバウム定数のそれなりの桁数の値でもって10の冪乗を計算したものが③になります。

ここで、第1ファイゲンバウム定数：4.6692016091029906718532としております。第1ファイゲンバウム定数の10000倍に近いですが、もう少し近付けてみたいですね(^_^)そこで、第2ファイゲンバウム定数が気になってきますね(^_^;)

10に第2ファイゲンバウム定数：2.5029078750958928222839を12373.68685844686で割ったものを加算して、それに対し第1ファイゲンバウム定数で冪乗したものが④の式になります。

第1ファイゲンバウム定数を10000倍したものにかなり近くなりましたね(^_^)

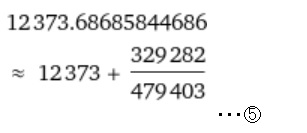
ここで、いきなり出てきた12373.68685844686について、第2ファイゲンバウム定数を用いて近似するため、かなり大きな値で割る必要があったのですが、その際に計算したところ、この値に落ち着きました。整数値部分を見ると、12373は素数で平方数の和（42^2 + 103^2）として1通りで表せる数です。⑤は12373.68685844686の有理数での近似式になります。

ここではもう少しひねりを加えて、値：12373.68685844686を左記の⑥のようなかたちで表現してみました。

ここでCLenはレンジェル定数と呼ばれる定数です。

⑥も用いて④を書き直したのが左記⑦になります。

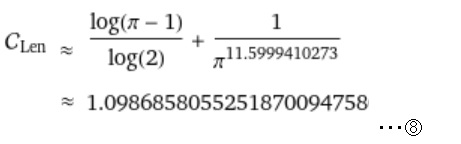
先ほど用いたレンジェル定数は⑧に示すような近似式もあります。

πの11乗に近い値で割ったものを加えているのが何故か印象的です。

また、ファイゲンバウム定数は底を10とするチャンパーノウン数C10と相性がよいようで、左記⑨、⑩のような近似式が得られました。

面白いのは、①にあらわれる5および32561、②にあらわれる443ですが、ともにソフィー・ジェルマン素数と呼ばれる素数になっていることです。また、①の32561および②の197は双子素数の片割れでもあります。

偶然って凄いですね～(^_^;)

ただの思いつきで試してみたものですが、ロジスティック写像の分岐図に現れるファイゲンバウム定数が10という一見何の変哲もない数と不思議な繋がりがあるように感じられて面白いですね(^_^)