
微細構造定数について調べていた頃、Wikipediaに掲載されていた「ほとんど整数」という項目で左記のような式(①とします)が掲載されておりました。確かに、20にかなり近いですね。そしてこの式は幾人かの学者により調べられたようですが、おそらく、偶然だろうということになっているようです。そこで気になって自分で調べてみることにしました(^_^)
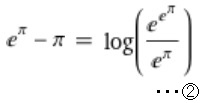
ここでπ=log(e^π)とも書けるので、①の式の左辺は左記のようにlog( )のカッコ内の除算の式として表せますね(これを②とします)。②のようなかたちで、他の値も調べたくなりますよね(^_^)
そこで、π - log(π)の値を調べてみることにしました。
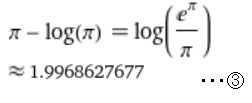
すると、③のような結果になり、2に近い値をとります。偶然なんでしょうね(^_^)
では、さらにlog(π) - log(log(π))はどうなるか見てみましょう。
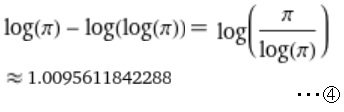
結果は④のように1に近い値をとります。やはり偶然なんでしょうね(^_^;)
では、log(log(π)) - log(log(log(π)))の値はどうなるかというと、log(log(log(π)))が負の値であるため、結果は2.1364・・・となり、整数に近い値はとりません。

そこで、 log(log(log(π)))が負の値をとる(すなわち、eの冪乗にかたちにすると小数点以下の値になる)ような小さな値については、(敢えてeではなく)慣れ親しんだ(10進数である)10の冪乗で表現したらどうなるか興味がわきますよね(自分だけかもしれませんが・・・)(^_^;)
すると、その結果は⑤のように、微細構造定数(α)の逆数(1/α)の値:137.084・・・に近い値をとります。偶然とはいえちょっと驚きましたね(^_^;)

⑤の式において、より微細構造定数の逆得値(1/α)により近付けるには、冪乗の数に手を加えるか、底となる10に手を加えるわけですが、10に小さな値:0.00468・・・を加えて計算した結果が⑥になります。
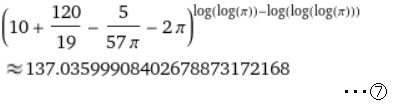
⑥の0.00468・・・の近似式として120/19 - 5/(57 π) - 2 πを用いたものが左記の⑦の式となります。

ここで、120/19 - 5/(57 π) - 2 πの内で120/19 - 5/(57 π)をeの冪乗としたときの値はどうなるか気になって計算してみました(eの冪乗で2πとかあると、何か波の周期のような気がしてしまって・・・)(^_^;)すると、整数:538に近い値となりました。

また、この120/19 - 5/(57 π) - 2 πを左記のように(負の)冪乗としていろいろな値で計算すると、左記⑨のようにほとんど整数といってよいような数が散見されます。
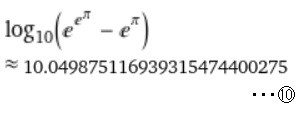
ここで話を①のe^π - πに戻しましょう。
e^π - π = log(e^(e^π)/e^π)であり、e^(e^π)を計算してみるとeの冪乗の冪乗(超冪)になっており、値があまりにも大きいのでe^(e^π) - e^πを計算してもほとんど整数のような値にはなりません(小数点以下の値があまり意味をなさないんでしょうね)。
そこで、「巨大な値には常用対数が便利」ということで、ここでも敢えて底をeではなく10とした対数で計算してみます。すると左記の⑩のような10に近い値になります。
偶然とはいえ、不思議ですね~(^_^)
ここまでくると、普段何気なく使用してる10という数自体が、実は不思議な数なのではないかと思えてきました(^_^;)

そこで、よせばいいの既存の結果からヒントを得て10という数値を素数の総乗の式で表してみたのが左記の⑪です。ここでPnはn番目の素数を表しております。W( )は乗積対数関数でW(1)は0.567・・・程の値をとり、オメガ定数と呼ばれるものになります。W(1)は式の定義よりネイピア数eと関連した数になります。C10は底を10とするチャンパーノウン数です。
分子と分母で±1の違いのみの対象形になっており、キレイなかたちですね(^_^)
そういえば忘れてましたが、最初に挙げてた①のe^π - π自体が(e^π - π)/2 ≒9.9995499・・・でしたね(^_^;)
eとπおよび微細構造定数と素数が10という数字と不思議な繋がりを持っているように思えてきますよね(^_^)
コメントをお書きください