微細構造定数 近似式(自作式)
ここでは物理の定数として有名な「微細構造定数 (Fine-structure constant)」(無次元の定数で記号としてはαで表示)を物理定数ではなく数学の定数を使って自作した近似式を掲載しております。また、近似式を求める課程で見つけたことなどについては、別途ブログで掲載しております。
但し、所詮は素人の自作式ですので、厳密な理論に基づいて導出しているわけではありません。要は「勘」あるのみです(^^;)
今まで作成した式の中で、なんとなくそれっぽく見えるものを選んで、その式が醸し出すあやしげな雰囲気を味わうのも一興かと思い掲載してみました。宜しければWolfram Alpha等で検算してみてくださいm(_ _)m
ちなみに、微細構造定数(α)の値としてはCODATAの推奨値(2018年)を用いており、
α:0.0072973525693
1/α:137.035999084
を基準としております。
以下掲載の式で使われているlog( )について、特にことわりがなければ自然対数関数を意味しております。また式の中で用いられているeは電気素量ではなくネイピア数を表しております(念のため・・・)。

tanh( )は双曲線正接関数です。
式の冪乗部分の右端のカッコ内のψはディガンマ関数で、そのカッコ内の式を計算するとエルデシュ・ボーウェイン定数(1.6066951...)と呼ばれる定数と同値になります。この定数はメルセンヌ数の逆数和になります。
上記の式はベルヌーイ数の母関数を冪乗したかたちをしております。単純に、上記母関数の変数に-πを代入し、それをπ+1乗すると、いきなり137に近い値が得られます。これが面白かったので、近似式を作ってみようと思った次第です。

微細構造定数の逆数値(1/α)の近似式を総乗のかたちで作成してみました。

微細構造定数(α)の近似式を総乗の式として作成してみました。
以降はαの近似式が掲載されております。
ここでEi( )は指数積分を表しており、Ei(-1)の値は-0.2193839・・・となります。

もう一つ総乗の式です。sech( )は双曲線正割関数です。無茶してますね(^_^;)
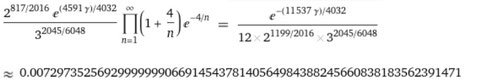
γはオイラー・マスケローニ定数です。
これは総乗の式に2,3,e等の冪乗の積を掛けて、さらに総乗の式を計算した結果になっております。総乗の式が上手いこと2,3,eの冪乗の積としてまとまったかな、と思っております。分母の12は3*2^2なので、それぞれ2および3の冪乗に組み込むこともできますが、見やすさとバランスを鑑みてこの状態にしております。

γはオイラー・マスケローニ定数です。
これも総乗の形式で自然対数関数と階乗の組み合わせですね。
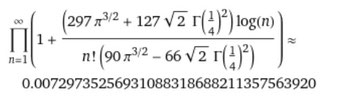
Γ( )はガンマ関数です。
上記の式と同じように自然対数関数と階乗の組み合わせです。

γはオイラー・マスケローニ定数です。
左記は総和のかたちです。nの階乗の逆数とn+1の階乗の逆数の差を基本構成として、そこにeおよびπの冪乗をnの係数としております。eおよびπをわざわざe^1およびπ^1として冪乗の数で表示しておりますが、単に見た目のバランスだけであって、それ以外の意味は特に無いです(^_^;)

左記も総和のかたちです。上記の式で外側に出ていた係数っぽい数式を和の中に組み込んでみました。
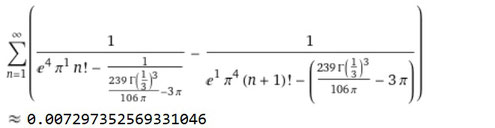
Γ( )はガンマ関数です。
上記の式の変形版ですね。

こちらはかなりシンプルにまとまってますね。
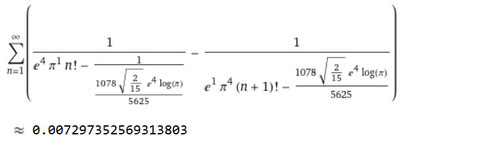
eの冪乗とlog(π)によりまとめたパターンですね。

前出の総和の式に対し、こちらはeの5乗とπの5乗を係数とした変数nを分母とした式で除算しているパターンですね。

上記の式のnの除算の部分でカッコ内の式が異なるパターンです。

こちらも上記と同様にカッコ内の式が異なるパターンです。

今度は少し趣を変えて、ガンマ関数Γ( )を分母に並べたかたちです。csc( )は余割関数です。

こちらもガンマ関数Γ( )を分母に並べたかたちです。割とコンパクトにまとまってますね(^_^)

再び総和のかたちです。sech( )は双曲線正割関数です。変数がnからkに変わっておりますが、若干この方が見やすいかな、程度の理由です(^_^;)但し、kは0から始まっております。また、分子はkの値により振動します。

同じく総和のかたちです。ζ( )はゼータ関数です。この場合、ゼータ関数はアペリーの定数になっております。

総和のかたちですが、上記の式で総和の外に出ていた係数部分の式を総和内に取り込んだかたちとなっております。ここでΦは黄金比の逆数(Φ=1/φ)を表しております。

これも上記と同じく総和のかたちですね。
ここで分子に現われる10^(2/5)という数はポグソン比という定数になります。

これも同様に総和のかたちです。
ここで分子に表れる179という数はソフィー・ジェルマン素数といわれる素数になります。

総和の式ですが、16k+11および17k+11の2乗を分母とする式のそれぞれの総和を合算しているかたちですね。
それぞれの総和をt:1-tの比で係数をかけて合算しております。ここでΦは黄金比の逆数(Φ=1/φ)を表しております。キレイなかたちですね(^_^)

こちらも総和の式で、上記と同様に16k+11および17k+11の2乗を分母としてそれぞれの総和を合算しているかたちです。
ここで(1/2; 1/4)∞は、1/4の乗積をqポッホハマー記号で表現しております。

こちらも総和の式です。
ここで係数部分に現われる2^(√2)ですが、ゲルフォント・シュナイダー定数といわれる定数になります。
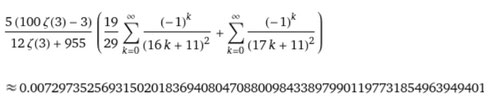
こちらも総和の式です。ζ( )はゼータ関数を表しています。ここでもゼータ関数はアペリーの定数になっております。
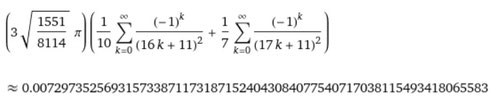
こちらも総和の式です。

こちらも総和の式です。

こちらも総和の式です。ここでC10は10を底とするチャンパーノウン数です。この総和のパターンの式は沢山あるのですが、キリがないのでこの辺でやめておきます(^_^;)

こちらも総和の式になりますが、より複雑ですね。
面白いのは、kの冪乗部分も含めて分母で±11を実施しているかたちになっているところですね。
総和の左から4および2、3の冪乗、eのγ(オイラー・マスケローニ定数)による冪乗がかけられておりますが、値としては1に近い(0.99724468・・・)ものです。
式としても値としてもなかなか美しいものだと思います(^^♪

j0,1は第1種ベッセル関数(α=0)の1番目の零点(根)を表しております。C10は10を底とするチャンパーノウン数です。
チャンパーノウン数の3乗にベッセル関数の根で表現された式を掛けております。
※ここで記載したαはベッセル関数の定義式の中で用いられている変数です。

φは黄金比でΦは黄金比の逆数です。C10は10を底とするチャンパーノウン数です。ここでKinは左下の総乗の式で与えられる内接多角形の定数です。左記の式ではこのKinの近似値を代入して算出しております。

ここから連分数での式になります。本当は無限大までの連分数としたかったのですが、計算できませんでした(^_^;)
nは1000までとなっておりますが、2000で計算しても微細構造定数の値としては大勢に影響はないので、よしとしております。おそらく、無限大としても成り立つかと・・・(^_^;)
ここで、φは黄金比、δsは白銀比(貴金属比の方)です。

連分数の式です。φは黄金比、δsは白銀比(貴金属比)を表しております。
上記の式の変形版ですね。

連分数の式です。φは黄金比、δsは白銀比(貴金属比)を表しております。γはオイラー・マスケローニ定数です。
この式では、分子に三角関数の和、分母に黄金比および白銀比の積の冪乗というかたちになっております。

連分数の式です。φは黄金比、δsは白銀比(貴金属比)を表しております。上記では分子は三角関数の和でしたが、この式では積になっております。

連分数の式です。φは黄金比、δsは白銀比(貴金属比)を表しております。sec( )は正割関数です。上記の式と異なるのは、分母が黄金比と白銀比の積の冪乗と定数項との差になっている点ですね。

連分数の式です。φは黄金比、δsは白銀比(貴金属比)を表しております。γはオイラー・マスケローニ定数です。Γ( )はガンマ関数です。こちらも二つ上の式と似たかたちになっております。

連分数の式です。Cはカタラン定数(0.91596559・・・)です。
eおよびπで極力表現してみた式ですね。

これも連分数の式ですが、θはミルズ定数です。一見ゴチャゴチャしてますが、3という数字で割とキレイにまとまってますね(^_^)

こちらも連分数の式ですが、CAはアルティンの定数です。
分かり難いですが、分子はアルティンの定数と変数nの積です。

これも連分数の式で、CAはアルティンの定数です。
上記の式とは、分母の部分に三角関数が使われている点が異なりますね。

これも連分数の式で、CAはアルティンの定数です。
上記の式とは、分母の部分の定数項の式が異なります。

これも連分数の式で、CAはアルティンの定数でφは黄金比です。ここで(-1/φ^2; -1/φ^2)∞は、-1/φ^2の乗積をqポッホハマー記号で表現しており、この値はフィボナッチの階乗定数と呼ばれるものになります。

これも連分数の式で、CAはアルティンの定数でφは黄金比です。
W( )は乗積対数関数で、W(1)はオメガ定数と呼ばれるものでありその値は0.567143・・・となります。また、coth( )は双曲線余接関数で、csch( )は双曲線余割関数です。
黄金比を組み込んだかたちです。

これも連分数の式で、CAはアルティンの定数でθはミルズ定数です。Γ( )はガンマ関数で、coth( )は双曲線余接関数です。
ミルズ定数の値は前の式で用いた値よりも桁数が短いですが、前に用いた値だと今回の場合、桁数が長すぎて計算できなかったようで、少し短くしております(^_^;)

これも連分数の式で、CCEはコープランド・エルデシュ定数です。γはオイラー・マスケローニ定数で、
coth( )は双曲線余接関数です。割とコンパウクトにまとまってますね。

こちらも連分数の式で、Cはカタラン定数(0.91596559・・・)で、φは黄金比です。

これも連分数の式ですが、分子がレムニスケート周率と言われる定数の式になります。φは黄金比でΓ( )はガンマ関数になります。

連分数の式です。φは黄金比でΓ( )はガンマ関数になります。
Kinは内接多角形の定数です。分子はレムニスケート周率を表す式になっております。

連分数の式です。φは黄金比でΓ( )はガンマ関数になります。
ζ( )はゼータ関数です。
分子はレムニスケート周率を表す式になっております。このかたちは値の精度も良いので、バリエーションが豊富です(^_^;)

連分数の式です。φは黄金比でΓ( )はガンマ関数になります。
coth( )は双曲線余接関数です。
分子はレムニスケート周率を表す式になっております。

連分数の式です。φは黄金比でΓ( )はガンマ関数になります。
coth( )は双曲線余接関数です。
分子はレムニスケート周率を表す式になっております。
上記の式とほぼ同じですが、分母の係数部分の式が異なります。

連分数の式です。φは黄金比でΓ( )はガンマ関数になります。
coth( )は双曲線余接関数です。
分子はレムニスケート周率を表す式です。
この式では、coth( )に掛かっていた係数部分を定数項として分離したかたちになっております。

連分数の式です。φは黄金比でΓ( )はガンマ関数になります。
coth( )は双曲線余接関数です。
分子はレムニスケート周率を表す式です。
上記の式との違いは分母の定数項部分ですが、ガウス定数を表す式(Γ(1/4)^2/(2*π^(3/2)*√2)を含んでおります。

連分数の式です。φは黄金比でΓ( )はガンマ関数になります。
coth( )は双曲線余接関数です。
分子はレムニスケート周率を表す式です。

連分数の式です。φは黄金比でΓ( )はガンマ関数になります。
coth( )は双曲線余接関数です。
分子はレムニスケート周率を表す式です。

連分数の式です。φは黄金比でΓ( )はガンマ関数になります。
coth( )は双曲線余接関数です。Aはグレイシャー・キンケリン定数(1.2824271・・・)と言われる定数です。
分子はレムニスケート周率を表す式です。
この定数項のパターンは他にもかなりありますが、キリがないのでこれくらいにしておきます(^_^;)

連分数の式です。φは黄金比でΓ( )はガンマ関数になります。
coth( )は双曲線余接関数です。
分子はレムニスケート周率を表す式です。
上記の式との違いは分母の定数項をなくして、黄金比の冪乗に吸収させた点ですね。

連分数の式です。φは黄金比でΓ( )はガンマ関数になります。
coth( )は双曲線余接関数です。
分子はレムニスケート周率を表す式です。
この式でもそうですが、微細構造定数を近似する式では素数、特に11という数字をよく見かけます。11の倍数もよく見かけます。
やっぱり不思議な数なんでしょうかね。

連分数の式です。δsは白銀比(貴金属比)です。
分子のPは素数定数という定数値(10進数値)で、変数nとの積になっております。

連分数の式です。δsは白銀比(貴金属比)です。
分子のPは素数定数(10進数値)です。
素数定数を分子とした式ですが、上記の式とは分子/分母ともにことなるかたちです。

連分数の式です。φは黄金比、δsは白銀比(貴金属比)です。
C10は10を底とするチャンパーノウン数です。Kinは内接多角形の定数です。

連分数の式です。φは黄金比、δFは第1ファイゲンバウム定数、αFは第2ファイゲンバウム定数、C10は10を底とするチャンパーノウン数で、Kinは内接多角形の定数です。
黄金比の3乗を分母とする分子の式の部分にもαFが出てきて面白いですね(^_^)
※この場合も含め、以降で使用するファイゲンバウム定数は差分方程式がZ=2のとき、つまりロジスティック写像の場合における値を指します。

この式は、黄金比φの冪乗および10を底とするチャンパーノウン数C10の3乗の積で表現されております。
Pは素数定数(10進数値)です。

δFは第1ファイゲンバウム定数、αFは第2ファイゲンバウム定数、C10は10を底とするチャンパーノウン数で、Kinは内接多角形の定数です。また、j0,1は第1種ベッセル関数(α=0)の1番目の零点(根)を表しております。
※ここで記載したαはベッセル関数の定義式の中で用いられている変数です。
この式は、δFの冪乗およびC10とKinの2乗の積で表現したものです。冪乗の式の中にαFがひょっこり出てきてますね(^_^)

総和の式ですが、2の冪乗にベルヌーイ数をかけてnの階乗で割ったかたちになっております。
以降、このようなかたちの式が続きます。

こちらも総和の式です。先ほどは2の冪乗でしたが、ここではπの冪乗のかたちになっております。

こちらも総和の式です。黄金比:φの冪乗のかたちになっております。

総和の式で、白銀比(貴金属比):δsの冪乗のかたちになっております。
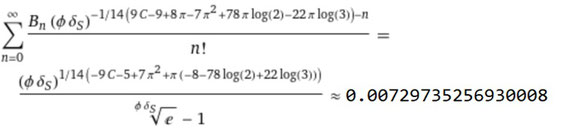
総和の式で、黄金比と白銀比の積の冪乗のかたちになっております。

総和の式で、黄金比と白銀比の和の冪乗のかたいになっております。

総和の式で、レムニスケート周率を2倍したものの冪乗のかたちになっております。Im(ρ1)はリーマンゼータ関数の自明ではない1番目の零点の虚部を表しております。
なかなか面白いかたちですね。

総和の式で、先ほどと同様にレムニスケート周率を2倍したものの冪乗のかたちの異なるバージョンです。

総和の式で、第2ファイゲンバウム定数の近似値であるπ + tan ^(-1)(e^π)の冪乗のかたちになっております。

総和の式で、φは黄金比です。
レムニスケート周率を2倍にしたものから約0.121ほどの値を引いており、それを冪乗したかたちになっております。
その約0.121ほどの値がqポッホハマー記号(-1/φ^2; -1/φ^2)∞で表現されており、この値はフィボナッチの階乗定数と呼ばれるものになります。
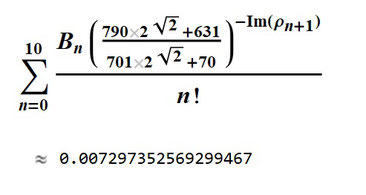
n=10までの総和の式です。比較的収束がはやく面白いので掲載してみました。
本当はn→∞とすると管理人の計算環境では警告が出るからなんですけどね(^_^;)
Im(ρn)はリーマンゼータ関数の自明ではないn番目の零点の虚部を表しております。n=50やn=100としても微細構造定数の値的には大勢に影響はないですね(^_^)

qポッホハマー記号(-1/φ^2; -1/φ^2)∞で表現されたフィボナッチの階乗定数が式の冒頭部分にきております。面白い式ですね(^_^)